|
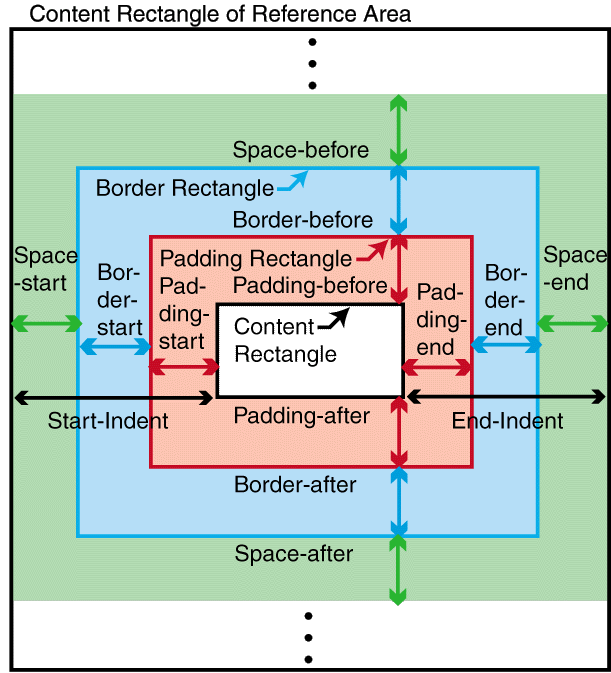
4 Area ModelIn XSL, one creates a tree of formatting objects that serve as inputs or specifications to a formatter. The formatter generates a hierarchical arrangement of areas which comprise the formatted result. This section defines the general model of areas and how they interact. The purpose is to present an abstract framework which is used in describing the semantics of formatting objects. It should be seen as describing a series of constraints for conforming implementations, and not as prescribing particular algorithms. 4.1 IntroductionThe formatter generates an ordered tree, the area tree, which describes a geometric structuring of the output medium. The terms child, sibling, parent, descendant, and ancestor refer to this tree structure. The tree has a root node. Each area tree node other than the root is called an area and is associated to a rectangular portion of the output medium. Areas are not formatting objects; rather, a formatting object generates zero or more rectangular areas, and normally each area is generated by a unique object in the formatting object tree. NOTE: An area has a content-rectangle, the portion in which its child areas are assigned, and optional padding and border. The diagram shows how these portions are related to one another. The outer bound of the border is called the border-rectangle, and the outer bound of the padding is called the padding-rectangle.
Each area has a set of traits, a mapping of names to values, in the way elements have attributes and formatting objects have properties. Individual traits are used either for rendering the area or for defining constraints on the result of formatting, or both. Traits used strictly for formatting purposes or for defining constraints may be called formatting traits, and traits used for rendering may be called rendering traits. Traits whose values are copied or derived from a property of the same or a corresponding name are listed in [C Property Summary] and [5 Property Refinement / Resolution]; other traits are listed below. NOTE: The semantics of each type of formatting object that generates areas are given in terms of which areas it generates and their place in the area-tree hierarchy. This may be further modified by interactions between the various types of formatting objects. The properties of the formatting object determine what areas are generated and how the formatting object's content is distributed among them. (For example, a word that is not to be hyphenated may not have its glyphs distributed into areas on two separate line-areas.) The traits of an area are either: 1. "directly-derived" -- The values of directly-derived traits are the computed value of a property of the same or a corresponding name on the generating formatting object, or 2. "indirectly-derived" -- The values of indirectly-derived traits are the result of a computation involving the computed values of one or more properties on the generating formatting object, other traits on this area or other interacting areas (ancestors, parent, siblings, and/or children) and/or one or more values constructed by the formatter. The calculation formula may depend on the type of the formatting object. This description assumes that refined values have been computed for all properties of formatting objects in the result tree, i.e., all relative and corresponding values have been computed and the inheritable values have been propagated as described in [5 Property Refinement / Resolution]. This allows the process of inheritance to be described once and avoids a need to repeat information on computing values in this description. The indirectly-derived traits are: block-progression-direction, inline-progression-direction, shift-direction, glyph-orientation, is-reference-area, is-viewport-area, left-position, right-position, top-position, bottom-position, left-offset, top-offset, is-first, is-last, alignment-point, area-class, start-intrusion-adjustment, end-intrusion-adjustment, generated-by, returned-by, page-number, blink, underline-score, overline-score, through-score, underline-score-color, overline-score-color, through-score-color, alignment-baseline, baseline-shift, nominal-font, dominant-baseline-identifier, actual-baseline-table, and script. 4.2 Rectangular AreasThere are two types of areas: block-areas and inline-areas. These differ according to how they are typically stacked by the formatter. An area can have block-area children or inline-area children as determined by the generating formatting object, but a given area's children must all be of one type. Although block-areas and inline-areas are typically stacked, some areas can be explicitly positioned. A line-area is a special kind of block-area whose children are all inline-areas. A glyph-area is a special kind of inline-area which has no child areas, and has a single glyph image as its content. Typical examples of areas are: a paragraph rendered by using an fo:block formatting object, which generates block-areas, and a character rendered by using an fo:character formatting object, which generates an inline-area (in fact, a glyph-area). Associated with any area are two directions, which are derived from the generating formatting object's writing-mode and reference-orientation properties: the block-progression-direction is the direction for stacking block-area descendants of the area, and the inline-progression-direction is the direction for stacking inline-area descendants of the area. Another trait, the shift-direction, is present on inline-areas and refers to the direction in which baseline shifts are applied. Also the glyph-orientation defines the orientation of glyph-images in the rendered result. If the reference-orientation for an area is 0, then the top, bottom, left, and right edges of the content are parallel to those of the area's parent and consistent with them. Otherwise the edges are rotated from those of the area's parent as described in [7.19.3 "reference-orientation"]. The inline-progression-direction and block-progression-direction are determined by the location of these edges as described in [7.26.7 "writing-mode"]. The Boolean trait is-reference-area determines
whether or not an area establishes a coordinate system for
specifying indents. An area for which this trait is The Boolean trait is-viewport-area determines
whether or not an area establishes an opening through which its
descendant areas can be viewed, and can be used to
present clipped or scrolled material; for example, in printing
applications where bleed and trim is desired.
An area for which this trait is A common construct is a viewport/reference pair. This is a block-area viewport-area V and a block-area reference-area R, where R is the sole child of V and where the start-edge and end-edge of the content-rectangle of R are parallel to the start-edge and end-edge of the content-rectangle of V. Each area has the traits top-position, bottom-position,
left-position, and right-position which represent the distance
from the edges of its content-rectangle to the like-named edges of the
nearest ancestor reference-area (or the page-viewport-area
in the
case of areas generated by descendants of formatting objects
whose absolute-position is The block-progression-dimension and inline-progression-dimension of an area represent the extent of the content-rectangle of that area in each of the two relative dimensions. |
|
Other traits include:
Unless otherwise specified, the traits of a formatting object are present on each of its generated areas, and with the same value. (However, see sections [4.7.2 Line-building] and [4.9.4 Border, Padding, and Background].) As described above, the content-rectangle is the rectangle bounding the inside of the padding and is used to describe the constraints on the positions of descendant areas. It is possible that marks from descendant glyphs or other areas may appear outside the content-rectangle. Related to this is the allocation-rectangle of an area, which is used to describe the constraints on the position of the area within its parent area. For an inline-area this is either the normal-allocation-rectangle or the large-allocation-rectangle. The normal-allocation-rectangle extends to the content-rectangle in the block-progression-direction and to the border-rectangle in the inline-progression-direction. The large-allocation-rectangle is the border-rectangle. Unless otherwise specified, the allocation-rectangle for an area is the normal-allocation-rectangle.
Allocation- and content-rectangles of an inline-area |
|
Large-allocation-rectangle of an inline-area For a block-area, the allocation-rectangle extends to the border-rectangle in the block-progression-direction and outside the content-rectangle in the inline-progression-direction by an amount equal to the end-indent, and in the opposite direction by an amount equal to the start-indent. NOTE:
Allocation- and content-rectangles of a block-area The edges of a rectangle are designated as follows:
For purposes of this definition, the content-rectangle of an area uses the inline-progression-direction and block-progression-direction of that area; but the border-rectangle, padding-rectangle, and allocation-rectangle use the directions of its parent area. Thus the edges designated for the content-rectangle may not correspond to the same-named edges on the padding-, border-, and allocation-rectangles. This is important in the case of nested block-areas with different writing-modes. The following diagram shows the correspondence between the various edge names for a mixed writing-mode example:
Each inline-area has an alignment-point determined by the formatter, on the start-edge of its allocation-rectangle; for a glyph-area, this is a point on the start-edge of the glyph on its alignment baseline (see below). This is script-dependent and does not necessarily correspond to the (0,0) coordinate point used for the data describing the glyph shape. In the area tree, the set of areas with a given parent is ordered. The terms initial, final, preceding, and following refer to this ordering. In any ordered tree, this sibling order extends to an ordering of the entire tree in at least two ways.
"Preceding" and "following", when applied to non-siblings, will depend on the extension order used, which must be specified. However, in either of these given orders, the leaves of the tree (nodes without children) are unambiguously ordered. This section defines the notion of block-stacking constraints and inline-stacking constraints involving areas. These are defined as ordered relations, i.e., if A and B have a stacking constraint it does not necessarily mean that B and A have a stacking constraint. These definitions are recursive in nature and some cases may depend upon simpler cases of the same definition. This is not circularity but rather a consequence of recursion. The intention of the definitions is to identify areas at any level of the tree which have only space between them. The area-class trait is an enumerated value which is
Block-stacking constraints If P is a block-area, then there is a fence preceding P if P is a reference-area or if the border-before-width or padding-before-width of P are non-zero. Similarly, there is a fence following P if P is a reference-area or if the border-after-width or padding-after-width of P are non-zero. If A and B are stackable areas, and S is a sequence of space-specifiers (see [4.3 Spaces and Conditionality]), it is defined that A and B have block-stacking constraint S if any of the following conditions holds:
NOTE:
Adjacent Edges with Block-stacking When A and B have a block-stacking constraint, the adjacent edges of A and B are an ordered pair recursively defined as:
Block-stacking constraint example Example. In this diagram each node represents a block-area. Assume that all padding and border widths are zero, and none of the areas are reference-areas. Then P and A have a block-stacking constraint, as do A and B, A and C, B and C, C and D, D and B, B and E, D and E, and E and P; these are the only pairs in the diagram having block-stacking constraints. If B had non-zero padding-after, then D and E would not have any block-stacking constraint (though B and E would continue to have a block-stacking constraint). Inline-stacking constraints. This section will recursively define the inline-stacking constraints between two areas (either two inline-areas or one inline-area and one line-area), together with the notion of fence preceding and fence following; these definitions are interwoven with one another. This parallels the definition for block-stacking constraints, but with the additional complication that we may have a stacking constraint between inline-areas which are stacked in opposite inline-progression-directions. (This is not an issue for block-stacking constraints because a block-area which is not a reference-area may not have a block-progression-direction different from that of its parent.) If P and Q have an inline-stacking constraint, then P has a fence preceding Q if P is a reference-area or has non-zero border-width or padding-width at the first adjacent edge of P and Q. Similarly, Q has a fence following P if Q is a reference-area or has non-zero border-width or padding-width at the second adjacent edge of P and Q. If A and B are normal areas, and S is a sequence of space-specifiers, it is defined that A and B have inline-stacking constraint S if any of the following conditions holds:
Adjacent Edges with Inline-stacking 1.
Adjacent Edges with Inline-stacking 2.
When A and B have an inline-stacking constraint, the adjacent edges of A and B are an ordered pair defined as:
|
|
Two areas are adjacent if they have a block-stacking constraint or an inline-stacking constraint. It follows from the definitions that areas of the same type (inline or block) can be adjacent only if all their non-common ancestors are also of the same type (up to but not including their nearest common ancestor). Thus, for example, two inline-areas which reside in different line-areas are never adjacent. An area A begins an area P if A is a descendant of P and P and A have either a block-stacking constraint or an inline-stacking constraint. In this case the second of the adjacent edges of P and A is defined to be a leading edge in P. A space-specifier which applies to the leading edge is also defined to begin P Similarly, An area A ends an area P if A is a descendant of P and A and P have either a block-stacking constraint or an inline-stacking constraint. In this case the first of the adjacent edges of A and P is defined to be a trailing edge in P. A space-specifier which applies to the trailing edge is also defined to end P Each script has its preferred "baseline" for aligning glyphs from that script. Western scripts typically use a "alphabetic" baseline that touches at or near the bottom of capital letters. Further, for each font there is a preferred way of aligning embedded glyphs from different scripts, e.g., for a Western font there are separate baselines for aligning embedded ideographic or Indic glyphs. Each block-area and inline-area has a dominant-baseline-identifier trait whose value is a baseline identifier corresponding to the type of alignment expected for inline-area descendants of that area, and each inline-area has an alignment-baseline which specifies how the area is aligned to its parent. These traits are interpreted as described in section [7.7.1 Fonts and Font Data]. For each font, an actual-baseline-table maps these identifiers to points on the start-edge of the area. By abuse of terminology, the line in the inline-progression-direction through the point corresponding to the dominant-baseline-identifier is called the "dominant baseline." 4.3 Spaces and ConditionalityA space-specifier is a compound datatype whose components are minimum, optimum, maximum, conditionality and precedence. Minimum, optimum, and maximum are lengths and can be used to define a constraint on a distance, namely that the distance should preferably be the optimum, and in any case no less than the minimum nor more than the maximum. Any of these values may be negative, which can (for example) cause areas to overlap, but in any case the minimum should be less than or equal to the optimum value, and the optimum less than or equal to the maximum value.
Conditionality is an enumerated value which controls whether a
space-specifier has effect at the beginning or end of a reference-area or a
line-area. Possible values are
Precedence has a value which is either an integer or the special
token Space-specifiers occurring in sequence may interact with each other. The constraint imposed by a sequence of space-specifiers is computed by calculating for each space-specifier its associated resolved space-specifier in accordance with their conditionality and precedence, as shown below in the space-resolution rules. The constraint imposed on a distance by a sequence of resolved space-specifiers is additive; that is, the distance is constrained to be no less than the sum of the resolved minimum values and no larger than the sum of the resolved maximum values. To compute the resolved space-specifier of a given space-specifier S, consider the maximal inline-stacking constraint or block-stacking constraint containing S. The resolved space-specifier of S is a non-conditional, forcing space-specifier computed in terms of this sequence.
Example. Suppose the sequence of space values occurring at the
beginning of a reference-area is:
first, a space with value 10 points (that is
minimum, optimum, and maximum all equal to 10 points) and conditionality
The padding of a block-area does not interact with any space-specifier (except that by definition, the presence of padding at the before- or after-edge prevents areas on either side of it from having a stacking constraint.) The border or padding at the before-edge or after-edge of a block-area may be specified as conditional. If so, then it is set to zero if its associated edge is a leading or trailing edge in a reference-area. In this case, the border or padding is taken to be zero for purposes of the stacking constraint definitions. The border or padding at the start-edge or end-edge of an inline-area may be specified as conditional. If so, then it is set to zero if its associated edge is a leading or trailing edge in a reference-area or line-area. In this case, the border or padding is taken to be zero for purposes of the stacking constraint definitions. |
|
NOTE: For each pair of normal areas B and B' in the subtree below P, if B and B' have a block-stacking constraint S, then the distance between the adjacent edges of B and B' is consistent with the constraint imposed by the resolved values of the space-specifiers in S.
Example. In the diagram, if area
A
has a space-after value of 3 points, B a
space-before
of 1 point, and C a space-before of 2 points, all
with
precedence of Intrusion adjustments (both start- and end-) are defined to account for the indentation that occurs as the result of side floats. If A and B are areas which have the same nearest reference area ancestor, then A and B are defined to be inline-overlapping if there is some line parallel to the inline-progression-direction, which intersects both the allocation-rectangle of A and the allocation-rectangle of B. If B is a block-area then its before-intrusion-allowance is defined to be the sum of the border-before-width and padding-before-width values of all areas which are ancestors of B and descendants of B's nearest ancestor reference-area. If A is an area of class If A is a block-area with float="start", then the start-intrusion value of A is the distance from the start-edge of the content-rectangle of the parent of A to the end-edge of the allocation-rectangle of A. If A is a block-area with float="end" then the end-intrusion value of A is the distance from the start-edge of the allocation-rectangle of A to the end-edge of the content-rectangle of the parent of A. If B is a block-area which is either
then the start-intrusion-adjustment is defined to be the maximum of the start-intrusion values of the areas which intrude on B. The end-intrusion-adjustment is defined to be the maximum of the end-intrusion values of the areas which intrude on B. If B is none of (1.), (2.) or (3.), then its start-intrusion-adjustment and end-intrusion-adjustment are defined to be zero. |
4.5 Line-areasA line-area is a special type of block-area, and is generated by the same formatting object which generated its parent. Line-areas do not have borders and padding, i.e., border-before-width, padding-before-width, etc. are all zero. Inline-areas are stacked within a line-area relative to a baseline-start-point which is a point determined by the formatter, on the start-edge of the line area's content-rectangle. The allocation-rectangle of a line is determined by the value of the
line-stacking-strategy trait: if the
value is The nominal-requested-line-rectangle for a line-area is the rectangle whose start-edge and end-edge are parallel to and coincident with the start-edge and end-edge of the content-rectangle of the parent block-area (as modified by typographic properties such as indents), whose before-edge is separated from the baseline-start-point by the text-altitude, and whose after-edge is separated from the baseline-start-point by the text-depth. It has the same block-progression-dimension for each line-area child of a block-area. The maximum-line-rectangle for a line-area is the rectangle whose start-edge and end-edge are parallel to and coincident with the start-edge and end-edge of the nominal-requested-line-rectangle, and whose extent in the block-progression-direction is the minimum required to enclose both the nominal-requested-line-rectangle and the allocation-rectangles of all the inline-areas stacked within the line-area; this may vary depending on the descendants of the line-area.
Nominal and Maximum Line Rectangles The per-inline-height-rectangle for a line-area is the rectangle whose start-edge and end-edge are parallel to and coincident with the start-edge and end-edge of the nominal-requested-line-rectangle, and whose extent in the block-progression-dimension is determined as follows. The expanded-rectangle of an inline-area is the rectangle with start-edge and end-edge coincident with those of its allocation-rectangle, and whose before-edge and after-edge are outside those of its allocation-rectangle by a distance equal to either (a.) the half-leading, when the area's allocation-rectangle is specified to be the normal-allocation-rectangle by the description of the generating formatting object , or (b.) the space-before and space-after (respectively), when the area's allocation-rectangle is specified to be the large-allocation-rectangle. The expanded-nominal-requested-line-rectangle is the rectangle with start-edge and end-edge coincident with those of the nominal-requested-line-rectangle, and whose before-edge and after-edge are outside those of the nominal-requested-line-rectangle by a distance equal to the half-leading. The extent of the per-inline-height-rectangle in the block-progression-direction is then defined to be the minimum required to enclose both the expanded-nominal-requested-line-rectangle and the expanded-rectangles of all the inline-areas stacked within the line-area; this may vary depending on the descendants of the line-area. NOTE: 4.6 Inline-areasAn inline-area has its own line-height trait, which may be
different from the line-height of its containing block-area. This may affect the
placement of its ancestor line-area when the line-stacking-strategy
is An inline-area may or may not have child areas, and if so it may or may not be a reference-area. The dimensions of the content-rectangle for an inline-area without children is computed as specified by the generating formatting object, as are those of an inline-area with block-area children. An inline-area with inline-area children has a content-rectangle which extends from its dominant baseline (see [4.2.6 Font Baseline Tables]) by its text-depth in the block-progression-direction, and in the opposite direction by its text-altitude; in the inline-progression-direction it extends from the start-edge of the allocation-rectangle of its first child to the end-edge of the allocation-rectangle of its last child. The allocation-rectangle of such an inline-area is the same as its content-rectangle. The allocation-rectangle of an inline-area without children is either the normal-allocation-rectangle or the large-allocation-rectangle, as specified in the description of the generating formatting object. NOTE: Examples of inline-areas with children might include portions of inline mathematical expressions or areas arising from mixed writing systems (left-to-right within right-to-left, for example). Inline-area children of an area are typically stacked in the inline-progression-direction within their parent area, and this is the default method of positioning inline-areas. Inline-areas are stacked relative to the dominant baseline, as defined above ([4.2.6 Font Baseline Tables]). For a parent area P whose children are inline-areas, P is defined to be properly stacked if all of the following conditions hold:
|
|
This section describes the ordering constraints that apply to formatting an fo:inline or similar inline-level object. An inline-level formatting object F which constructs one or more inline-areas does so by placing normal inline-areas and/or anchor inline-areas returned to F by its child formatting objects as children of inline-areas which it generates. For each such formatting object F, it must be possible to form an ordered partition P consisting of ordered subsets S1, S2, ..., Sn of the normal and/or anchor inline-areas returned by the child formatting objects, such that the following are all satisfied:
|
4.8 Keeps and BreaksKeep and break conditions apply to a class of areas, which are typically page-reference-areas, column-areas, and line-areas. The appropriate class for a given condition is referred to as a context and an area in this class is a context-area. As defined in Section [6.4.1 Introduction], page-reference-areas are areas generated by an fo:page-sequence using the specifications in a fo:page-master, and column-areas are normal-flow-reference-areas generated from a region-body, or region-reference-areas generated from other types of region-master. A keep or break condition is an open statement about a formatting object and the tree relationships of the areas it generates with the relevant context-areas. These tree relationships are defined mainly in terms of leading or trailing areas. If A is a descendant of P, then A is defined to be leading in P if A has no preceding sibling which is a normal area, nor does any of its ancestor areas up to but not including P. Similarly, A is defined to be trailing in P if A has no following sibling which is a normal area, nor does any of its ancestor areas up to but not including P. For any given formatting object, the next formatting object in the flow is the first formatting object following (in the pre-order traversal order) which generates and returns normal areas. Break conditions are either break-before or break-after conditions. A break-before condition is satisfied if the first area generated and returned by the formatting object is leading within a context-area. A break-after condition depends on the next formatting object in the flow; it is satisfied if either there is no such next formatting object, or if the first normal area generated and returned by that formatting object is leading in a context-area. Break conditions are imposed by the break-before and
break-after properties. A
refined value of Keep conditions are either keep-with-previous, keep-with-next, or keep-together conditions. A keep-with-previous condition on an object is satisfied if the first area generated and returned by the formatting object is not leading within a context-area, or if there are no preceding areas in a post-order traversal of the area tree. A keep-with-next condition is satisfied if the last area generated and returned by the formatting object is not trailing within a context-area, or if there are no following areas in a pre-order traversal of the area tree. A keep-together condition is satisfied if all areas generated and returned by the formatting object are descendants of a single context-area. Keep conditions are imposed by the "within-page", "within-column", and "within-line" components
of the "keep-with-previous", "keep-with-next", and
"keep-together" properties.
The refined value of each component specifies the strength of the keep condition
imposed, with higher numbers being stronger than lower numbers and the value
The area tree is constrained to satisfy all break conditions imposed. Each keep condition must also be satisfied, except when this would cause a break condition or a stronger keep condition to fail to be satisfied. If not all of a set of keep conditions of equal strength can be satisfied, then some maximal satisfiable subset of conditions of that strength must be satisfied (together with all break conditions and maximal subsets of stronger keep conditions, if any). |
4.9 Rendering ModelThis section makes explicit the relationship between the area tree and visually rendered output. Areas generate three types of marks: (1) the area background, if any, (2) the marks intrinsic to the area (a glyph, image, or decoration) if any, and (3) the area border, if any. An area tree is rendered by causing marks to appear on an output medium in accordance with the areas in the area tree. This section describes the geometric location of such marks, and how conflicts between marks are to be resolved. Each area is rendered in a particular location. Formatting object semantics describe the location of intrinsic marks relative to the object's location, i.e., the left, right, top, and bottom edges of its content-rectangle. This section describes how the area's location is determined, which determines the location of its intrinsic marks. For each page, the page-viewport-area corresponds isometrically to the output medium. The page-reference-area is offset from the page-viewport-area as described below in section [4.9.2 Viewport Geometry].
All areas in the tree with an area-class of Any area in the tree which is the child of a viewport-area is rendered as described in section [4.9.2 Viewport Geometry].
All other areas in the tree are positioned such that the
left-, right-, top-,
and bottom-edges of its content-rectangle are offset inward
from the
content-rectangle of its nearest ancestor reference-area by distances
specified by the left-position,
right-position, top-position,
and
bottom-position traits, respectively. These are shifted down
and left by the values of the top-offset
and left-offset traits, respectively, if the area
has a relative-position of A reference-area which is the child of a viewport-area is positioned such that the start-edge and end-edge of its content-rectangle are parallel to the start-edge and end-edge of the content-rectangle of its parent viewport-area. The start-edge of its content-rectangle is offset from the start-edge of the content-rectangle of its parent viewport-area by an inline-scroll-amount, and the before-edge of its content-rectangle is offset from the before-edge of the content-rectangle of its parent viewport-area by a block-scroll-amount.
If the block-progression-dimension of the reference-area is larger
than that
of the viewport-area and the overflow trait
for the reference-area is The visibility of marks depends upon the location of the marks, the visibility of the area, and the overflow of any ancestor viewport-areas.
If an area has visibility
If an area has an overflow of |
|
4.9.4 Border, Padding, and Background The border- and padding-rectangles are determined relative to the content-rectangle by the values of the common padding and border width traits (border-before-width, etc.). For any area, which is not a child of a viewport-area, the border is rendered between the border-rectangle and the padding-rectangle in accordance with the common border color and style traits. For a child of a viewport-area, the border is not rendered. For an area, which is not part of a viewport/reference pair, the
background is rendered. For an area that is either a viewport-area or a
reference-area in a viewport/reference pair, if the refined value of
background-attachment is The background, if any, is rendered in the padding-rectangle, in accordance with the background-image, background-color, background-repeat, background-position-vertical, and background-position-horizontal traits. For each class of formatting objects, the marks intrinsic to its generated areas are specified in the formatting object description. For example, an fo:character object generates a glyph-area, and this is rendered by drawing a glyph within that area's content-rectangle in accordance with the area's font traits and glyph-orientation and blink traits. In addition, other traits (for example the various score and score-color traits) specify other intrinsic marks. In the case of score traits (underline-score, overline-score and through-score), the score thickness and position are specified by the nominal-font in effect; where the font fails to specify these quantities, they are implementation-dependent. 4.9.6 Layering and Conflict of Marks Marks are layered as described below, which defines a partial ordering of which marks are beneath which other marks. Two marks are defined to conflict if they apply to the same point in the output medium. When two marks conflict, the one which is beneath the other does not affect points in the output medium where they both apply. Marks generated by the same area are layered as follows: the area background is beneath the area's intrinsic marks, and the intrinsic marks are beneath the border. Layering among the area's intrinsic marks is defined by the semantics of the area's generating formatting object and its properties. For example, a glyph-area's glyph drawing comes beneath the marks generated for text-decoration. The stacking layer of an area is defined by its stacking context and its z-index value. The stacking layer of an area A is defined to be less than that of an area B if some ancestor-or-self A' of A and B' of B have the same stacking context and the z-index of A' is less than the z-index of B'. If neither stacking layer is less than the other then they are defined to have the same stacking layer. If A and B are areas, and the stacking layer of A is less than the stacking layer of B, then all marks generated by A are beneath all marks generated by B. If A and B are areas with the same stacking layer, the backgrounds of A and B come beneath all other marks generated by A and B. Further, if A is an ancestor of B (still with the same stacking layer), then the background of A is beneath all the areas of B, and all the areas of B are beneath the intrinsic areas (and border) of A. If A and B have the same stacking layer and neither is an ancestor of the other, then it is an error if either their backgrounds conflict or if a non-background mark of A conflicts with a non-background mark of B. An implementation may recover by proceeding as if the marks from the first area in the pre-order traversal order are beneath those of the other area. 4.10 Sample Area Tree
|
||||||||
|
With any suggestions or questions please feel free to contact us | ||||||||